Logistic regression can fail with root mean squares

Logistic regression can fail with root mean squares#

Hide code cell content 
import numpy as np
import pandas as pd
pd.set_option('mode.copy_on_write', True)
import matplotlib.pyplot as plt
from scipy.optimize import minimize

We read in the mtcars dataset that will be very familiar to users of R:

mtcars = pd.read_csv('mtcars.csv')
mtcars.head()
mpg cyl disp hp drat wt qsec vs am gear carb
0 21.0 6 160.0 110 3.90 2.620 16.46 0 1 4 4
1 21.0 6 160.0 110 3.90 2.875 17.02 0 1 4 4
2 22.8 4 108.0 93 3.85 2.320 18.61 1 1 4 1
3 21.4 6 258.0 110 3.08 3.215 19.44 1 0 3 1
4 18.7 8 360.0 175 3.15 3.440 17.02 0 0 3 2

This dataset has one row per make and model of car. The columns have various measures and other information about each make and model.

The columns we are interested in here are:

  • mpg: Miles/(US) gallon

  • am: Transmission (0 = automatic, 1 = manual)

Notice that am is already numeric, and so is already a dummy variable.

mpg = mtcars['mpg']
am_dummy = mtcars['am']

We will try to predict whether the car has an automatic transmission (column am) using the miles per gallon measure (column mpg).

Here is a plot of the am values against the mpg values:

Hide code cell content 
# Code to make nice plots for binary columns.  Please ignore.
def plot_binary(df, x_name, bin_name, bin_labels=(0, 1),
                color_names=('red', 'blue')):
    x_vals = df[x_name]
    bin_vals = df[bin_name]
    # Build plot, add custom label.
    dummy = bin_vals.replace(bin_labels, (0, 1))
    colors = bin_vals.replace(bin_labels, color_names)
    plt.scatter(x_vals, dummy, c=colors)
    plt.xlabel(x_name)
    plt.ylabel('%s\n0 = %s, 1 = %s' % (x_name, bin_labels[0], bin_labels[1]))
    plt.yticks([0, 1]);  # Just label 0 and 1 on the y axis.
    # Put a custom legend on the plot.  This code is a little obscure.
    plt.scatter([], [], c=color_names[0], label=bin_labels[0])
    plt.scatter([], [], c=color_names[1], label=bin_labels[1])
Hide code cell content 
plot_binary(mtcars, 'mpg', 'am')
plt.legend();
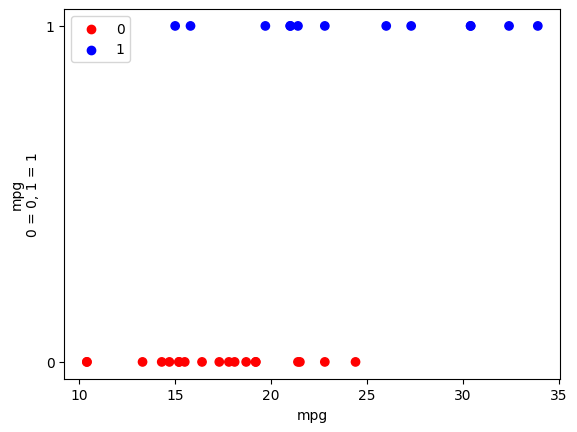
../_images/07076a4a7a19ff8a62a1655291c13c038a3914d56940cda70df652248f237e7b.png

We need our machinery for calculating the inverse logit transformation, converting from the log-odds-ratio straight line prediction to the sigmoid prediction.

def inv_logit(y):
    """ Reverse logit transformation
    """
    odds_ratios = np.exp(y)  # Reverse the log operation.
    return odds_ratios / (odds_ratios + 1)  # Reverse odds ratios operation.


def params2pps(intercept, slope, x):
    """ Calculate predicted probabilities of 1 for each observation.
    """
    # Predicted log odds of being in class 1.
    predicted_log_odds = intercept + slope * x
    return inv_logit(predicted_log_odds)

This is our simple sum of square cost function comparing the sigmoid p predictions to the 0 / 1 labels

def rmse_logit(c_s, x_values, y_values):
    # Unpack intercept and slope into values.
    intercept, slope = c_s
    # Predicted p values on sigmoid
    pps = params2pps(intercept, slope, x_values)
    # Prediction errors.
    sigmoid_error = y_values - pps
    # Root mean squared error
    return np.sqrt(np.mean(sigmoid_error ** 2))

We run minimize using some (it turns out) close-enough initial values for the log-odds intercept and slope:

# Guessed log-odds intercept slope of -5, 0.5
mr_rmse_ok = minimize(rmse_logit, [-5, 0.5], args=(mpg, am_dummy))
mr_rmse_ok

  message: Optimization terminated successfully.
  success: True
   status: 0
      fun: 0.39143665337028305
        x: [-6.164e+00  2.819e-01]
      nit: 16
      jac: [ 1.863e-08  2.533e-07]
 hess_inv: [[ 4.949e+02 -2.326e+01]
            [-2.326e+01  1.122e+00]]
     nfev: 72
     njev: 24

The prediction sigmoid looks reasonable:

inter_ok, slope_ok = mr_rmse_ok.x
predicted_ok = inv_logit(inter_ok + slope_ok * mpg)
Hide code cell content 
plot_binary(mtcars, 'mpg', 'am')
plt.scatter(mpg, predicted_ok, c='gold', label='SS fit, OK start')
plt.legend();
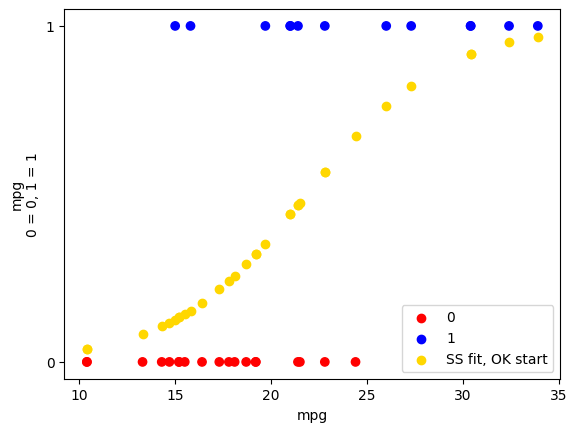
../_images/65c51b16d4080ddb9b944c2f0f80d65e3b31771ff9297d13e31d20de6d82cd60.png

But - if we start with a not-so-close initial guess for the intercept and slope, minimize gets terribly lost:

# Guessed log-odds intercept slope of 1, 1
mr_rmse_not_ok = minimize(rmse_logit, [1, 1], args=(mpg, am_dummy))
mr_rmse_not_ok

  message: Optimization terminated successfully.
  success: True
   status: 0
      fun: 0.6373774391990981
        x: [ 6.641e-01 -2.562e+00]
      nit: 1
      jac: [ 0.000e+00  0.000e+00]
 hess_inv: [[1 0]
            [0 1]]
     nfev: 33
     njev: 11

The prediction sigmoid fails completely:

inter_not_ok, slope_not_ok = mr_rmse_not_ok.x
predicted_not_ok = inv_logit(inter_not_ok + slope_not_ok * mpg)
Hide code cell content 
plot_binary(mtcars, 'mpg', 'am')
plt.scatter(mpg, predicted_not_ok, c='gold', label='RMSE fit, bad start')
plt.legend();
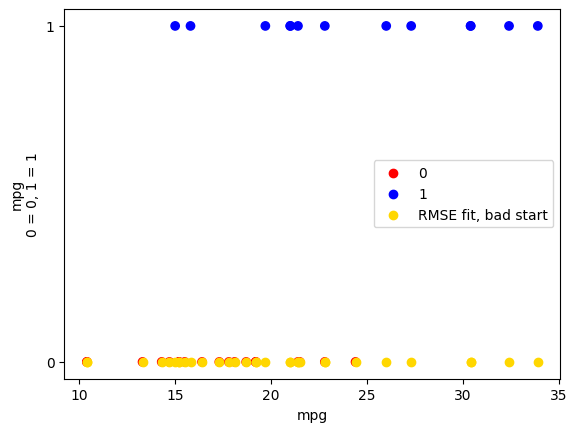
../_images/3d6d5c83d650c20dff2f90b1f001a9b97474c0397f0f39d72312114871abc412.png

Can we do better with the maximum likelihood estimate (MLE) cost function?

def logit_reg_cost(intercept_and_slope, x, y):
    """ Cost function for maximum likelihood
    """
    intercept, slope = intercept_and_slope
    pp1 = params2pps(intercept, slope, x)
    p_of_y = y * pp1 + (1 - y) * (1 - pp1)
    log_likelihood = np.sum(np.log(p_of_y))
    return -log_likelihood

Here we pass some absolutely terrible initial guesses for the intercept and slope:

mr_LL = minimize(logit_reg_cost, [10, -5], args=(mpg, am_dummy))
mr_LL

  message: Optimization terminated successfully.
  success: True
   status: 0
      fun: 14.837583824119367
        x: [-6.604e+00  3.070e-01]
      nit: 13
      jac: [-2.384e-07 -4.172e-06]
 hess_inv: [[ 5.538e+00 -2.659e-01]
            [-2.659e-01  1.330e-02]]
     nfev: 57
     njev: 19

The fit is still reasonable:

inter_LL, slope_LL = mr_LL.x
predicted_LL = inv_logit(inter_LL + slope_LL * mpg)

plot_binary(mtcars, 'mpg', 'am')
plt.scatter(mpg, predicted_LL, c='gold', label='LL prediction')
plt.legend();
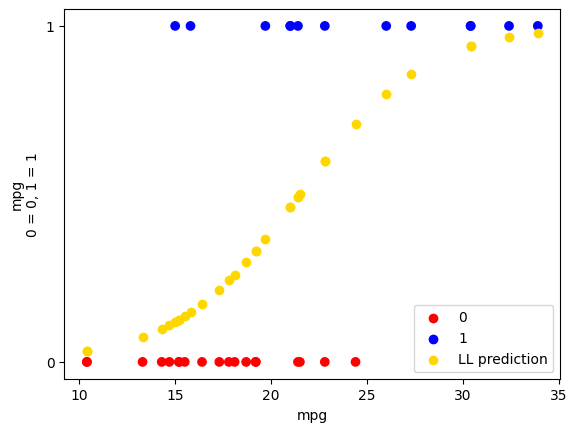
../_images/3cba567e38117ccc477edc43c4b37ec600723eb9cea0e2be0035a711d8c0a5b2.png

As we have seen before, the MLE fit above is the same algorithm that Statmodels and other packages use.

import statsmodels.formula.api as smf

model = smf.logit('am ~ mpg', data=mtcars)
fit = model.fit()
fit.summary()

Optimization terminated successfully.
         Current function value: 0.463674
         Iterations 6
Logit Regression Results
Dep. Variable: am No. Observations: 32
Model: Logit Df Residuals: 30
Method: MLE Df Model: 1
Date: Wed, 05 Jun 2024 Pseudo R-squ.: 0.3135
Time: 16:10:51 Log-Likelihood: -14.838
converged: True LL-Null: -21.615
Covariance Type: nonrobust LLR p-value: 0.0002317
coef std err z P>|z| [0.025 0.975]
Intercept -6.6035 2.351 -2.808 0.005 -11.212 -1.995
mpg 0.3070 0.115 2.673 0.008 0.082 0.532

Notice that the intercept and slope coefficients are the same as the ones we found with the MLE cost function and minimize.