Noble politics and comparing counts#
This page has two aims:
to practice and extend Pandas indexing;
to extend the idea of permutation to data in categories;
We also ask the question - is politics noble?
Show code cell content
# Our usual imports
import numpy as np
# Make random number generator.
rng = np.random.default_rng()
import pandas as pd
# Safe setting for Pandas. Needs Pandas version >= 1.5.
pd.set_option('mode.copy_on_write', True)
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
Our data is from this book:
Samuel P. Oliner and Pearl M. Oliner (1988) “The Altruistic Personality: Rescuers of Jews in Nazi Europe”. Free Press, New York.
See the dataset page for some more details.
The Oliners wanted to identify distinctive traits of people who rescued Jews in Nazi Europe. In order to do that, they collected structured interviews with 231 people for whom there was strong documentary evidence that they had sheltered Jews, despite considerable risk to themselves. These are the “rescuer” group in the table below. They also found 126 controls with roughly similar background, nationality, age and education. Of these, 53 claimed to have either sheltered Jews, or to have been active in the resistance. These are the “actives” group in the table. This leaves 73 controls who were not active, and the authors termed these “bystanders”.
The table below has data from table 6.8 of their book, where they break down the groups according to the answer they gave to the question “Did you belong to a political party before the war?”.
As usual, if you are running on your own computers, download the file
oliner_tab6_8a_1.csv to the same
directory as this notebook.
# Load the table
party_tab = pd.read_csv('oliner_tab6_8a_1.csv')
party_tab
| party_yn | rescuer | active | bystander | |
|---|---|---|---|---|
| 0 | Yes | 44 | 6 | 7 |
| 1 | No | 165 | 44 | 64 |
| 2 | out of | 209 | 50 | 71 |
Setting the index#
We have already seen Pandas indexing. We are going to be selecting data out of this table with indexing, and we would like to make the index (row labels) be as informative as possible. The current index, which Pandas created automatically, is sequential numbers, which are not memorable or informative.
party_tab.index
RangeIndex(start=0, stop=3, step=1)
Row labels need not be numbers. They can also be strings. Strings are often more useful in identifying the data in the rows.
We might prefer to use the values in the first column - party_yn as the
labels for the rows.
We can do this with the data frame set_index method. It replaces the current
index (the sequential numbers) with the data from a column.
# Replace the numerical index with the party_yn labels.
party_tab = party_tab.set_index('party_yn')
party_tab
| rescuer | active | bystander | |
|---|---|---|---|
| party_yn | |||
| Yes | 44 | 6 | 7 |
| No | 165 | 44 | 64 |
| out of | 209 | 50 | 71 |
Notice that Pandas took the party_yn column out of the data frame and used it
to replace the index.
This makes it easier to use the .loc attribute to select data, using row
labels. For example, we can select individual elements like this:
# How many rescuers were there, in total?
party_tab.loc['out of', 'rescuer']
209
The question#
Looking at the data in the table, it seems as if the Rescuers had a stronger tendency to belong to a political party than, say, the Bystanders.
To get more specific, we look at the proportion of Rescuers and Bystanders that answered Yes (to being a member of a political party before the war).
The out of row has the total number of people in each column.
# Proportion of Yes for Rescuers.
party_tab.loc['Yes', 'rescuer'] / party_tab.loc['out of', 'rescuer']
0.21052631578947367
# Proportion of Yes for Bystanders.
party_tab.loc['Yes', 'bystander'] / party_tab.loc['out of', 'bystander']
0.09859154929577464
That looks like a substantial difference - but could it have come about by chance?
Let’s put that another way - we see that 44 of 209 Rescuers have “Yes” to belonging to political party. Is 44 a larger number than we would expect by chance?
Cleaning up the table#
We start by selecting the data we need from the original table.
First we use loc indexing to specify that we want:
The rows labeled “No” and “Yes”;
The columns labeled “bystander” and “rescuer”.
bystander_tab = party_tab.loc[['No', 'Yes'], ['bystander', 'rescuer']]
bystander_tab
| bystander | rescuer | |
|---|---|---|
| party_yn | ||
| No | 64 | 165 |
| Yes | 7 | 44 |
For reflection: You could do the same operation with the .drop method.
How?
Notice the lists above ['Yes', 'No'] and ['bystander', 'rescuer']. These
specify the row labels and columns labels that we want.
Notice too that we have swapped the order of the rows (to “No” and “Yes” ) and
the columns (to “bystander” and “rescuer”). This is to better match the
output of pd.crosstab below. You may see what we mean when we get there.
Now we ask you to cast your eye to the bottom-right value of the table, and the value of interest — 44. This is the count for people who were both “rescuer” and said “Yes” to political party. We continue our search to see if this value is larger than we would expect by chance.
What do we mean by chance?#
Our question above was whether the observed proportions in the table could have come about by chance. As usual, our first step is to imagine an ideal (null) world where rescuers and bystanders have exactly the same tendency to belong to a political party. This is the null-model, often called the null hypothesis.
We will take random samples from this world, to see if the random samples look anything like the numbers we see in the actual data. If they do, then we might not be very interested in the differences we see, in the actual data, because the differences could plausibly have come about as a sample from an ideal world where there was no difference in tendency to belong to political parties.
So, how do we take samples from this ideal world?
We will take the same number of fake rescuers as there are real rescuers, and the same number of fake bystanders as there are real bystanders.
We will assume that the same number of people overall are not members of a political party:
# Number of people who did not belong to a political party.
n_no = bystander_tab.loc['No', 'rescuer'] + bystander_tab.loc['No', 'bystander']
n_no
229
This leaves the rest, who were a member of a political party:
# Number of people who did belong to a political party.
n_yes = bystander_tab.loc['Yes', 'rescuer'] + bystander_tab.loc['Yes', 'bystander']
n_yes
51
We can get the same numbers for “Yes” and “No” using the sum method of the
data frame, with the axis=1 argument, to tell sum to operate along the
columns (the second axis):
row_totals = bystander_tab.sum(axis=1)
row_totals
party_yn
No 229
Yes 51
dtype: int64
The total number of people represented in the table is the sum of the “Yes” and “No” counts:
row_totals.sum()
280
We therefore have 280 labels (51 Yes labels and 229 No labels) to assign to our 280 people (209 rescuers and 71 bystanders).
In our ideal world, this assignment to “Yes” and “No” is random. We can shuffle up the labels (“Yes”, “No”), and assign each person (rescuer, bystander) a shuffled (therefore, random) label. We take this fake pairing, and calculate the numbers in each of the four categories, to create a fake table, that is a random version of the actual table. If we do that many times, we can get an idea of how the numbers vary in the fake tables, and therefore, what randomness looks like, in this ideal world, of no association between rescuer / bystander and Yes / No.
Recreating the original data#
The bystander_tab table above gives the counts of people in each of the four
categories. We will call this the Counts Table.
To do the shuffling we need, we reconstruct a new people table that has one
row for each person represented in the Counts Table. We could also call this
the Observations Table. Instead of having the counts, it reconstructs the
individual entries that correspond to the counts.
There are 280 people represented in the Counts Table, of which:
64 are “No” for party membership and “bystander” for respondent type: (“No”, “bystander) label pair.
165 are (“No”, “rescuer”)
7 are “Yes” for party and “bystander” for respondent (“Yes”, “bystander”)
44 are (“Yes”, “rescuer”)
Let’s say that the people DataFrame has two columns, one for each label that can apply to a person.
The first column is party_yn and contains the “Yes” or “No” according to
whether that person was a member of a political party.
The second column is respondent and contains bystander if the person was a
bystander, and rescuer if they were a rescuer.
The people DataFrame would have:
64 rows with “No” in
party_ynand “bystander” inrespondent;165 rows with “No” in
party_ynand “rescuer” inrespondent;7 rows with “Yes” in
party_ynand “bystander” inrespondent;44 rows with “Yes” in
party_ynand “rescuer” inrespondent;
Our approach will be to make a DataFrame that contains all four possible label pairs, and then repeat each of the rows by their respective counts (64, 165, 7, 44).
the DataFrame with the four possible label pairs.
We will do that using a list of lists.
Here is a list with the first label pair.
first_label_pair = ['No', 'bystander']
first_label_pair
['No', 'bystander']
We want to make a DataFrame that starts with 64 of these pairs. We can do this using the pd.DataFrame constructor with a list of lists. For example, here we make a new DataFrame with two rows,
first_two_pairs = [first_label_pair, first_label_pair]
first_two_pairs
[['No', 'bystander'], ['No', 'bystander']]
len(first_two_pairs)
2
first_two_pairs[0]
['No', 'bystander']
first_two_pairs[1]
['No', 'bystander']
In fact we can make multiple copies of a list by using the multiply (*) operator, like this:
# Multiply on a list means 'replicate'.
my_list = [1, 2]
my_list * 4
[1, 2, 1, 2, 1, 2, 1, 2]
another_list = [99]
another_list * 3
[99, 99, 99]
Notice that multiply (*) behaves completely differently for arrays:
# Multiply on an array means elementwise multiplication.
my_array = np.array([1, 2])
my_array * 4
array([4, 8])
Now we can replicate the initial pair with a list of lists and multiplication:
first_three_pairs = [first_label_pair] * 3
first_three_pairs
[['No', 'bystander'], ['No', 'bystander'], ['No', 'bystander']]
The reason this is useful, is that we can then use the pd.DataFrame constructor to convert the list of lists into rows of a DataFrame:
# Using a list of lists to define first three rows of DataFrame
first_three_rows = pd.DataFrame(first_three_pairs)
first_three_rows
| 0 | 1 | |
|---|---|---|
| 0 | No | bystander |
| 1 | No | bystander |
| 2 | No | bystander |
With that simple call, the DataFrame has default column labels of 0 and 1. We
can specify more useful and memorable column labels with the columns=
argument to the pd.DataFrame constructor:
first_three_rows = pd.DataFrame(first_three_pairs,
columns=['party_yn', 'respondent'])
first_three_rows
| party_yn | respondent | |
|---|---|---|
| 0 | No | bystander |
| 1 | No | bystander |
| 2 | No | bystander |
We want our new observations DataFrame to start with 64 observations. Remember, 64 is the count for the label combination of ‘No’, ‘bystander’:
bystander_tab.loc['No', 'bystander']
64
no_bystander_row_list = [['No', 'bystander']] * 64
# Show the first 5 lists in the list of lists
no_bystander_row_list[:5]
[['No', 'bystander'],
['No', 'bystander'],
['No', 'bystander'],
['No', 'bystander'],
['No', 'bystander']]
# Convert the list of lists into a DataFrame
no_bystander_observations = pd.DataFrame(
no_bystander_row_list,
columns=['party_yn', 'bystander'])
no_bystander_observations
| party_yn | bystander | |
|---|---|---|
| 0 | No | bystander |
| 1 | No | bystander |
| 2 | No | bystander |
| 3 | No | bystander |
| 4 | No | bystander |
| ... | ... | ... |
| 59 | No | bystander |
| 60 | No | bystander |
| 61 | No | bystander |
| 62 | No | bystander |
| 63 | No | bystander |
64 rows × 2 columns
How do we add the next 165 rows, with label pair ‘No’, ‘rescuer’:
bystander_tab.loc['No', 'rescuer']
165
We first make the list of lists corresponding to the rows:
no_rescuer_row_list = [['No', 'rescuer']] * 165
# Show the first 5 lists in the list of lists.
no_rescuer_row_list[:5]
[['No', 'rescuer'],
['No', 'rescuer'],
['No', 'rescuer'],
['No', 'rescuer'],
['No', 'rescuer']]
Next we use another aspect of lists - addition. As multiplication of a list replicates the elements in the list, so addition appends the elements of one list to another:
# Addition of two lists appends the second list to the first.
my_list = [1, 2]
another_list = [99, 100]
my_list + another_list
[1, 2, 99, 100]
Remember, this is different from addition with arrays, which does elementwise addition:
# Addition of two arrays gives elementwise addition.
my_array = np.array([1, 2])
another_array = np.array([99, 100])
my_array + another_array
array([100, 102])
If we add the first list of lists to the second list of lists, we get the 64 + 165 lists, and therefore, 64 + 165 rows.
both_no_row_list = no_bystander_row_list + no_rescuer_row_list
len(both_no_row_list)
229
both_no_observations = pd.DataFrame(both_no_row_list,
columns=['party_yn', 'respondent'])
both_no_observations
| party_yn | respondent | |
|---|---|---|
| 0 | No | bystander |
| 1 | No | bystander |
| 2 | No | bystander |
| 3 | No | bystander |
| 4 | No | bystander |
| ... | ... | ... |
| 224 | No | rescuer |
| 225 | No | rescuer |
| 226 | No | rescuer |
| 227 | No | rescuer |
| 228 | No | rescuer |
229 rows × 2 columns
Let’s assemble the whole observations DataFrame in one go:
row_lists = (
# The No rows
[['No', 'bystander']] * bystander_tab.loc['No', 'bystander'] +
[['No', 'rescuer']] * bystander_tab.loc['No', 'rescuer'] +
# The Yes rows
[['Yes', 'bystander']] * bystander_tab.loc['Yes', 'bystander'] +
[['Yes', 'rescuer']] * bystander_tab.loc['Yes', 'rescuer']
)
len(row_lists)
280
# The first 5 lists:
row_lists[:5]
[['No', 'bystander'],
['No', 'bystander'],
['No', 'bystander'],
['No', 'bystander'],
['No', 'bystander']]
# The last 5 lists
row_lists[-5:]
[['Yes', 'rescuer'],
['Yes', 'rescuer'],
['Yes', 'rescuer'],
['Yes', 'rescuer'],
['Yes', 'rescuer']]
Now we can construct the observations DataFrame from the list of lists that define the rows.
# Make the rows for "party_yn" and "bystander" by repeating rows from pairs.
people = pd.DataFrame(row_lists,
columns=['party_yn', 'respondent'])
people
| party_yn | respondent | |
|---|---|---|
| 0 | No | bystander |
| 1 | No | bystander |
| 2 | No | bystander |
| 3 | No | bystander |
| 4 | No | bystander |
| ... | ... | ... |
| 275 | Yes | rescuer |
| 276 | Yes | rescuer |
| 277 | Yes | rescuer |
| 278 | Yes | rescuer |
| 279 | Yes | rescuer |
280 rows × 2 columns
We check the counts in the people data frame by doing some row selection. For
example, to check we really do have 64 rows with the label “No” in party_yn
and “bystander” in respondent, we could do this:
no_rows = people[people['party_yn'] == 'No']
no_bystander_rows = no_rows[no_rows['respondent'] == 'bystander']
len(no_bystander_rows)
64
Luckily, Pandas has a crosstab function that does this counting work for us,
for all four combinations of “Yes”, “No” and “bystander”, “rescuer”.
people_tab = pd.crosstab(people['party_yn'], people['respondent'])
people_tab
| respondent | bystander | rescuer |
|---|---|---|
| party_yn | ||
| No | 64 | 165 |
| Yes | 7 | 44 |
As we hoped, the pd.crosstab on the people data frame regenerates the
counts Table we started with.
We have used pd.crosstab to reconstruct the Counts Table from our
Observations Table.
The null world#
The null or ideal world for our question is a world where the pairing of the
party_yn “Yes” / “No” labels and the respondent “bystander” / “rescuer”
labels are random.
We can make a data frame from that world doing a random shuffle of the
party_yn labels in our Observations Table, so the pairing of the party_yn
and respondent labels is random.
First pull out the party_yn and respondent columns for later use.
party_yn = people['party_yn']
respondent = people['respondent']
Remember, the crosstab of these columns gives the original count table:
pd.crosstab(party_yn, respondent)
| respondent | bystander | rescuer |
|---|---|---|
| party_yn | ||
| No | 64 | 165 |
| Yes | 7 | 44 |
Next, shuffle the party_yn values.
shuffled_party = rng.permutation(party_yn)
# Show the first ten values
shuffled_party[:10]
array(['No', 'No', 'No', 'Yes', 'Yes', 'No', 'Yes', 'No', 'Yes', 'No'],
dtype=object)
Show the new shuffled party_yn values with the original respondent labels:
fake_people = pd.DataFrame()
fake_people['party_yn'] = shuffled_party
fake_people['respondent'] = respondent
fake_people
| party_yn | respondent | |
|---|---|---|
| 0 | No | bystander |
| 1 | No | bystander |
| 2 | No | bystander |
| 3 | Yes | bystander |
| 4 | Yes | bystander |
| ... | ... | ... |
| 275 | No | rescuer |
| 276 | Yes | rescuer |
| 277 | No | rescuer |
| 278 | No | rescuer |
| 279 | No | rescuer |
280 rows × 2 columns
By the way — we only care about the random pairing between party_yn and
respondent. We shuffled party_yn above, but we could instead have shuffled
respondent, or both; any of these would generate a random pairing.
We now need the counts of people in each category. That is we need counts for:
‘No’ paired with ‘bystander’
‘Yes’ paired with ‘bystander’
‘No’ paired with ‘rescuer’
‘Yes’ paired with ‘rescuer’
For example, remember we are particularly interested in the combination of “Yes” and “rescuer”.
fake_tab = pd.crosstab(shuffled_party, respondent)
fake_tab
| respondent | bystander | rescuer |
|---|---|---|
| row_0 | ||
| No | 56 | 173 |
| Yes | 15 | 36 |
We saw in the original data that the rescuers seemed to have a greater tendency to belong to a political party. Let us restrict our attention to the count of “Yes” and “rescuer”.
That count, in our original Counts Table, was:
actual_y_resc = bystander_tab.loc['Yes', 'rescuer']
actual_y_resc
44
The equivalent count in our new fake Counts Table is:
fake_y_resc = fake_tab.loc['Yes', 'rescuer']
fake_y_resc
36
We need more random samples to see if the fake value is often as large as the real value. If so, then the ideal world, where the association between “Yes” / “No, and “bystander” / “rescuer” is random, is a reasonable explanation of what we see in the real world, and we might not want to investigate these data much further.
Unfortunately, pd.crosstab is horribly slow, so we need to drop our usual
number of iterations to 1000 to keep the run-time down.
counts = np.zeros(1000)
for i in np.arange(1000):
# Make a fake Observations Table by shuffling one set of labels.
shuffled_party = rng.permutation(party_yn)
# Get the Counts Table from the fake Observations Table.
fake_tab = pd.crosstab(shuffled_party, respondent)
# Store the count of interest.
counts[i] = fake_tab.loc['Yes', 'rescuer']
# Show the first 10 counts.
counts[:10]
array([39., 38., 33., 41., 37., 39., 40., 27., 38., 42.])
Here is our sampling distribution from sampling in the ideal world:
plt.hist(counts);
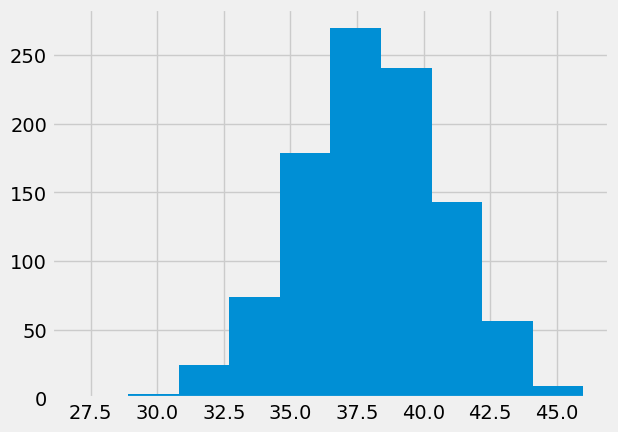
How unusual is the actual value, in this ideal world?
# Proportion of times we see ideal world sample >= actual value.
p_lte = np.count_nonzero(counts >= actual_y_resc) / len(counts)
p_lte
0.025
Very similar to Fisher’s exact test#
The Fisher’s exact test is the test that Fisher invented for the Lady Tasting Tea problem.
import scipy.stats as sps
# alternative='greater' actually refers to the probability that a sampling
# distribution top-left value will be greater than or equal to the observed
# top-left value, but for reasons given below, this is the same as the test
# on the bottom-right value, that we are interested in.
odds_ratio, p_val = sps.fisher_exact(bystander_tab, alternative='greater')
p_val
0.02267232069219596
Like the Chi-squared test#
Another common test for this sort of situation is the Chi-squared test.
The Chi-squared test tests the table values against the null hypothesis that there is no (null, not-any) tendency for (in our case) the Party membership labels to differ between the Rescuer and Bystander groups.
# Standard Chi-squared test, without Yates correction for 2x2 tables.
chi2_val, p_val, degf, expected = sps.chi2_contingency(people_tab,
correction=False)
p_val
0.03474922601463277
The Chi-squared test is asking a slightly different question from our original test. Our original test was a one-tailed test, in the sense that it has a direction. We are specifically interested in whether the null-world generates values as low as 44, but we were not interested in whether the null-world generates values that are greater than those we would expect by chance. The Chi-squared test is against a null-world where there is no deviation from random association in either direction. Hence the not-directional Chi-squared test has a higher probability than our directional randomization test, because we have to allow for chance deviations in either direction.
A question for reflection#
Now look at this. Here I do the same test, but I am looking at both of these counts, for each trial:
“Yes”, “rescuer”.
“No”, “bystander”.
# Yes, rescuer
counts_y_resc = np.zeros(1000)
# No, rescuer
counts_n_by = np.zeros(1000)
for i in np.arange(1000):
# Make a fake Observations Table by shuffling one set of labels.
shuffled_party = rng.permutation(party_yn)
fake_data = people.copy()
fake_data['party_yn'] = shuffled_party
# Get the Counts Table from the fake Observations Table.
fake_tab = pd.crosstab(fake_data['party_yn'], fake_data['respondent'])
# Store the "Yes" / "rescuer" count.
counts_y_resc[i] = fake_tab.loc['Yes', 'rescuer']
# Also store the "No" / "bystander" count.
counts_n_by[i] = fake_tab.loc['No', 'bystander']
Here are the values of the “Yes” / “rescuer” counts for the first 10 trials.
# First ten Yes rescuer counts
counts_y_resc[:10]
array([38., 36., 37., 37., 37., 41., 41., 40., 38., 39.])
These are the corresponding “No” / “bystander” counts:
# First ten No bystander counts
counts_n_by[:10]
array([58., 56., 57., 57., 57., 61., 61., 60., 58., 59.])
You may notice that they go up and down in exactly the same way. When the “Yes” / “rescuer” count goes up or down by 1, so does the “No” / “bystander” count - and the same is true for any change in the values; +1, +2, +3 …, -1, -2, -3 …
Therefore, the difference between the counts on each trial is always the same. In our case, the difference is -20:
# The difference between the counts for each trial is always the same.
count_diff = counts_y_resc - counts_n_by
print('First 10 differences', count_diff[:10])
print("Differences all the same?")
np.all(count_diff == count_diff[0])
First 10 differences [-20. -20. -20. -20. -20. -20. -20. -20. -20. -20.]
Differences all the same?
True
If we know the “Yes” / “rescuer” value, we can get the corresponding “No” / “bystander” value by subtracting -20 (in our particular case).
This means that if we calculate the corresponding p values for the “Yes” / “rescuer” or “No” / “bystander” counts, they are exactly the same.
# Proportion of times we see ideal world sample >= actual value.
p_lte_y_resc = np.count_nonzero(counts_y_resc >= actual_y_resc) / len(counts)
p_lte_y_resc
0.016
The test for “No”, “bystander” follows.
# Proportion of times we see ideal world sample >= actual value.
actual_n_by = bystander_tab.loc['No', 'bystander']
p_lte_n_by = np.count_nonzero(counts_n_by >= actual_n_by) / len(counts)
p_lte_n_by
0.016
See if you can work out why these counts go up and down in exactly the same way, on each trial. Why does this mean that the p values must be the same?
After a little reflection, have a look at the 2 by 2 tables page.